Aktuelles
- Diese Seite ist in den Learning-Campus umgezogen!
 MATERIALIEN zur Vorlesung.
MATERIALIEN zur Vorlesung.
Referenzen
- [T] "Mathematik für Informatiker", Band 1 von Gerald und Susanne Teschl, Springer (Leseprobe)
- [W] "Konkrete Mathematik (nicht nur) für Informatiker", Edmund Weitz, Springer
- [JL] Videos von Jörn Loviscach (https://www.youtube.com/user/JoernLoviscach)
- [CS] Videos von Christian Spannagel (https://www.youtube.com/user/pharithmetik)
- Hinweis: Viele Bücher bekommen Sie als eBook kostenlos über die Hochschule:
- über OPAC im Netzwerk der Hochschule, von zu Hause über VPN
- auf der Springer-Verlag-Seite: "Log in" > "Log in via Shibboleth or Athens" > "find your institution (via Shibboleth)" > "Technische Hochschule Rosenheim"
Weitere Infos
Studienstart
- Mathe-Vorkurse: von Jörn Loviscach oder OMB+, siehe auch www.fh-rosenheim.de/studienvorbereitung.html
- Grundlegende Software zum Studium von Jörn Loviscach, insbesondere:
- Wolfram-α: Doku/Beispiele, Doku/Beispiele Maths
- Erfahrungen zum Studium: Wir haben Studierende höherer Semester befragt…
- Wieviel Zeit sollte ich in einem Bachelor-Studium aufwenden? Workload-Berechnung nach Bologna...
- Beratung: Studiengang und übergreifend, soziale und psychologische Beratung
Tipps zu den Lernmaterialien
- Der Ordner MATERIALIEN wird über die Hochschul-Cloud (LRZ Sync+Share) bereitgestellt.
- mit Ordner auf Festplatte synchronisieren: Windows-PC, Linux-PC, MAC
- Android (Google PlayStore), iOS (Apple App-Store)
- Info unter: https://www.fh-rosenheim.de/intranet/einrichtungen/rechenzentrum/it-services/zentrale-speichermoeglichkeiten/hochschul-cloud/
- Watch YouTube videos with higher speed
Inverted Classroom
- Inverted Classroom:
- Inverted Classroom als moderne digitale Lehrmethode (auf YouTube) 3:09
- https://de.wikipedia.org/wiki/Umgedrehter_Unterricht
- Workload-Berechnung von Mathe 1 nach Bologna (7 CP = 210h Arbeit):
- Präsenz: 6h/Woche (6h*15 = 90h)
- Selbststudium: 8h/Woche (8h*15 = 120h)
Weiterführende Empfehlungen
- BSI - Technische Richtlinie: Kryptographische Verfahren: Empfehlungen und Schlussellängen
- MOOC: Web-Engineering I: Grundlagen der Web-Entwicklung auf iversity
- MOOC: Web-Engineering II: Entwicklung mobiler HTML5-Apps auf iversity
- MOOC: Algorithmen und Datenstrukturen mit Java auf iversity
- Interaktiv Coden lernen (z.B. Java, JavaScript, HTML/CSS, Command Line): codecademy.com
- Empfehlungen für das kommende SS:
- Bitte machen Sie sich fit für Mathe 2: Analysis und lineare Algebra, d.h. Niveau FOS-Technik: z.B. mit Vorkurs OMB+ oder Jörn Loviscach s.o.
- Als Vorbereitung für Programmieren 2 in Java: https://www.bigdev.de/p/cjava.html
Vorlesung - Inhalt und Termine
| Organisatorisches... | Di 5.10. |
| Grundlagen | |
|---|---|
| 1. Logik | V1: Fr 8.10. V2: Di 12.10. |
| 2. Mengen | V3: Fr 15.10. |
| 3. Funktionen | V4: Di 19.10., V5: Fr 22.10. |
| Vollständige Induktion und Rekursion | |
| 4. Vollständige Induktion | V6: Di 26.10. |
| 5. Rekursion | V7: Fr 29.10. |
| Zahlentheorie und Kryptographie | |
| 6. Stellenwertsysteme | V8: Di 2.11. |
| 7. Teilbarkeit und Primzahlen | V9: |
| 8. Primzahl-Klassiker - Hauptsatz der elementaren Zahlentheorie - Sieb des Eratosthenes - Satz des Euklid | V10: Fr 12.11. |
| 9. ggT und kgV | V11: Di 16.11. |
| 10. Euklidischer Algorithmus | V12: Fr 19.11. |
| 11. Diophantische Gleichungen | V13: Di 23.11. |
| 12. Kongruenzen und Restklassen | V14: Fr 26.11., V15: Di 30.11. |
| 13. Algebraische Strukturen | V16: Fr 3.12. |
| 14. Sätze von Euler und Fermat | V17: Di 7.12. |
| 15. Der chinesische Restsatz | V18: Fr 10.12. |
| 16. Kryptographie - Cäsar-Verschlüsselung - Vigenère-Verschlüsselung - RSA | V19: Di 14.12. |
| Probeklausur: Bitte bearbeiten Sie die Probeklausur vorab, wiederholen Themen bei Wissenslücken und bereiten Fragen vor! 👍 | Fr 17.12. |
Im folgenden Abschnitt brauchen Sie unbedingt das Vorwissen aus der Schule. Wenn Sie schon in der Schule Probleme mit Funktionen (Polynome, Wurzeln, e^x, ln(x), sin(x), cos(x), tan(x) usw.) und deren Rechenregeln (Potenzgesetze, Additionstheoreme usw.) hatten, dann bitte diese Themen mit Vorkurs von Jörn Loviscach oder OMB+ durcharbeiten.
| |
| Relationen und Funktionen | |
| 17. Relationen | V20: Di 21.12. |
| 18. Eigenschaften von Funktionen; lineare Funktionen; Potenz- und Wurzelfunktionen | |
| 19. Exponentialfunktionen, Logarithmen, Eulersche Zahl | V21: Di 11.1. |
| 20. Polynome | V22: Fr 14.1. |
| 21. Sinus und Freunde, Arcusfunktionen | |
| Übungen in Vorlesung, Probeklausur 2: Wir bearbeiten die Probeklausur gemeinsam in Breakoutsessions. Fragestunde | Di 18.1., Fr 21.1. Di 25.1. |
Semesterferien/nach der Prüfung: Bitte machen Sie sich fit für Mathe 2, d.h. Niveau FOS-Technik: Vorkurs von Jörn Loviscach oder OMB+
| |
Vorlesung 1 - Logik
- Skript namens "01a_Logik-Skript.pdf" unter MATERIALIEN
- YouTube Playlist (erster Teil: Logik 1-7)
- Logik 01 - Intro (08:34)
- Logik 02 - Aussagen (05:35)
- Logik 03 - Umgangssprache und Wahrheitstafeln (08:24)
- Logik 04 - Verknüpfungen von Aussagen (12:22)
- Logik 05 - Rechenregeln (10:02)
- Logik 06 - Prädikate (05:56)
- Logik 07 - Quantoren (15:15)
- Bitte meinen Kanal abonnieren und die 🔔 drücken (Liken 👍 und kommentieren 😊):
Vorlesung 2 - Logik Anwendungen
- Skript namens "01b_Logik-Anwendungen-Skript.pdf" unter MATERIALIEN
- YouTube Playlist (zweiter Teil: Logik-Anwendungen 1-11)
- Logik-Anwendungen 01 - Entwurf von Schaltkreisen: Logikgatter NICHT-, UND-, ODER-Gatter nach IEC/ANSI (4:21)
- Logik-Anwendungen 02 - Entwurf von Schaltkreisen: NAND-Gatter und weitere Übung (4:38)
- Logik-Anwendungen 03 - Entwurf von Schaltkreisen: Disjunktive Normalform (DNF) mit zwei Parametern (4:09)
- Logik-Anwendungen 04 - Entwurf von Schaltkreisen: Disjunktive Normalform (DNF) von XOR und XOR-Gatter (8:15)
- Logik-Anwendungen 05 - Entwurf von Schaltkreisen: Disjunktive Normalform (DNF) mit drei Parametern (2:38)
- Logik-Anwendungen 06 - Logik in der Programmierung: Wahrheitswerte false/true in C und Java, Demo in IDE (4:45)
- Logik-Anwendungen 07 - Logik in der Programmierung: Verknüpfungen UND, ODER, NICHT in C und Java (1:02)
- Logik-Anwendungen 08 - Logik in der Programmierung: Beispiel 1 - Auswertung einer Aussage in C (3:04)
- Logik-Anwendungen 09 - Logik in der Programmierung: Bitweise logische Operatoren UND, ODER in C und Java (1:27)
- Logik-Anwendungen 10 - Logik in der Programmierung: Beispiel 2 - If-Bedingung auswerten (2:26)
- Logik-Anwendungen 11 - Logik in der Programmierung: Beispiel 3 - If-Bedingung vereinfachen (mit Absorption) (2:49)
Ergänzungen (optional):
Vorlesung 3 - Mengen
- Skript namens "02_Mengen-Skript.pdf" unter MATERIALIEN
- Mengen 01 - Zahlenmengen: Natürliche, ganze und rationale Zahlen (03:33) [JL]
- Mengen 02 - Zahlenmengen: Reelle Zahlen (4:54) [JL]
- Mengen 03 - Zahlenmengen: Intervalle reeller Zahlen (02:41) [JL]
- Mengen 04 - Konzept (erst ab 5:47 min.!) (14:51) [CS]
- Mengen 05 - Konzept (13:29) [CS]
- Mengen 06 - Mengenoperationen (14:59) [CS]
- Mengen 07 - Mengenoperationen (14:58) [CS]
- Mengen 08 - Mengenoperationen (nur bis 6:00 min.!) (14:13) [CS]
- Mengen 09 - Übung: De Morgan (12:29) [CS]
- Quiz zu Mengen: Testen Sie Ihr Wissen...
Vorlesung 4 - Funktionen, Teil 1
- Bearbeiten Sie das Skript "03_Funktionen-Skript.pdf" (S. 1-11, bis einschließlich des Abschnitts "Wichtige Beispiele") mit Hilfe von "03_Funktionen-Skript-Vorlage.pdf". Beides finden Sie unter MATERIALIEN/1_Skripte.
Vorlesung 5 - Funktionen, Teil 2
- Bearbeiten Sie das Skript "03_Funktionen-Skript.pdf" (S. 12-17, ab Abschnitt "Verknüpfung") mit Hilfe von "03_Funktionen-Skript-Vorlage.pdf". Beides finden Sie unter MATERIALIEN/1_Skripte.
Vorlesung 6 - Vollständige Induktion
- Skript namens "04_Vollständige_Induktion-Skript.pdf" unter MATERIALIEN.
- Vollständige Induktion 01 - Prinzip (ab 05:05 min.) (9:38) [CS]
- Vollständige Induktion 02 - Übung (14:05) [CS]
- Vollständige Induktion 03 - Bubblesort-Algorithmus (10:54) [CS]
- Vollständige Induktion 04 - Gaußsche Summenformel, Teil 1 (14:52) [CS]
- Vollständige Induktion 05 - Gaußsche Summenformel, Teil 2 (14:46) [CS]
- Vollständige Induktion 06 - Gaußsche Summenformel, Teil 3 (03:33) [CS]
Vorlesung 7 - Rekursion
- Skript namens "05_Rekursion-Skript.pdf" unter MATERIALIEN.
- Rekursion 01 - Fakultät (ab 2:41 bis 5:27) (2:46) [JL]
- Rekursion 02 - Fibonacci-Zahlen (13:19) [CS]
- Rekursion 03 - Fibonacci-Zahlen Übung (06:45) [CS]
- optional: weitere Entdeckungen (Übungen) zu den Fibonacci-Zahlen mit Lösungen [CS]
- Rekursion 04 - Türme von Hanoi (01:45)
- Die Themen
- Rekursion - Türme von Hanoi
- Rekursion - Sparplan
Vorlesung 8 - Stellenwertsysteme
- Skript namens "06_Stellenwertsysteme-Skript.pdf" unter MATERIALIEN.
- Historisches (optional): https://youtu.be/ukabTKY7Org (15:00) [CS]
- Stellenwertsysteme 01 - Dezimalsystem (ab 4:41 min.) (10:11) [CS]
- Stellenwertsysteme 02 - Dezimal-, Oktal-, Hexadezimalsystem (15:05) [CS]
- Stellenwertsysteme 03 - Oktal-, Hexadezimalsystem (11:29) [CS]
- Stellenwertsysteme 04 - Binärsystem (08:57) [CS]
- Stellenwertsysteme 05 - Hornerschema (14:59) [CS]
- Anwendung von Binär-, Hexadezimal- und Oktalsystem:
- Bild: LCD Pixel, https://commons.wikimedia.org/wiki/File%3ALcd.jpg
- Bild: RGB-Codierung in HTML im Hexadezimalsystem, z.B. #00FF00 ist Grün: https://wiki.selfhtml.org/wiki/Grafik/Farbpaletten
- Text: ASCII-Codierung in Hexadezimaldarstellung (z.B. 0x20 ist Leerzeichen, in C liefert char a = 0x41; ein 'A' ), https://de.wikipedia.org/wiki/American_Standard_Code_for_Information_Interchange
- Zahlen: int in C in Binärdarstellung (negative Zahlen im Zweierkomplement, z.B. -1 wird als 1111 1111 1111 1111 1111 1111 1111 1111 dargestellt, bei 32-bit int), Demo mit Debugger. Nachlesen z.B. in [C von A bis Z, Kap.5.2]
- In UNIX-Systemen werden Dateiberechtigungen mit drei Oktalziffern beschrieben, z.B. 777 heißt jeder darf alles: siehe Übung
Vorlesung 9 - Teilbarkeit und Primzahlen
- Skript namens "07_Teilbarkeit_und_Primzahlen-Skript.pdf" unter MATERIALIEN.
- Teilbarkeit und Primzahlen 01 - Teilbarkeit (09:06) [CS]
- Teilbarkeit und Primzahlen 02 - Teilermengen und Primzahlen (ab 1:50 min.) (12:21)[CS]
- Teilbarkeit und Primzahlen 03 - Ein Äquivalenzbeweis zu Teilermengen (ab 3:04 min.) (11:56) [CS]
- Teilbarkeit und Primzahlen 04 - Primfaktorzerlegung (09:29) [CS]
Ergänzungen:
- Tabelle der Primzahlen < 100.000 oder
- Primes <= 1.000.000 with Sieve of Eratosthenes in C - siehe nächste Vorlesung :-)
- Was ist ein Googol?
- Hilberts Hotel: verschiedene Videos dazu:
- Hilberts Hotel, Zahlen und Unendlichkeiten (DorFuchs) 11:12
- Hilberts Hotel (Spannagel) 7:46
- Das Paradoxon des Unendlichen Hotels - Jeff Dekofsky (englisch) 5:59
- Wie einem unendlichen Hotel die Zimmer ausgingen (englisch) 6:06
Vorlesung 10 - Primzahl-Klassiker
- Skript namens "08_Primzahl-Klassiker-Skript.pdf" unter MATERIALIEN.
- Primzahl-Klassiker 01 - Hauptsatz der elementaren Zahlentheorie - Teil 1 (ab 0:44 min) (14:10) [CS]
- Primzahl-Klassiker 02 - Hauptsatz der elementaren Zahlentheorie - Teil 2 (14:43) [CS]
- Primzahl-Klassiker 03 - Hauptsatz der elementaren Zahlentheorie - Teil 3 (14:17) [CS]
- Primzahl-Klassiker 04 - Sieb des Eratosthenes (14:56) [CS]
- Primzahl-Klassiker 05 - Satz des Euklid (12:57) [CS]
- Ausblick (optional): Primzahlzwillinge (06:52) [CS]
Ergänzungen:
- Primes <= 1.000.000 with Sieve of Eratosthenes in C
- siehe auch Bilder zu Primzahlen: https://www.mathematik.uni-muenchen.de/~forster/primes.html
Vorlesung 11 - ggT und kgV
- Skript namens "09_ggT_und_kgV-Skript.pdf" unter MATERIALIEN.
- ggT und kgV 01 - Vielfachenmenge (05:17) [CS]
- ggT und kgV 02 - kgV (07:40) [CS]
- ggT und kgV 03 - ggT (09:32) [CS]
- ggT und kgV 04 - ggT und PFZ (14:04) [CS]
- ggT und kgV 05 - ggT und kgV (05:18) [CS]
Vorlesung 12 - Euklidischer Algorithmus
- Skript namens "10_Euklidischer_Algorithmus-Skript.pdf" unter MATERIALIEN.
- Euklidischer Algorithmus 01 - Division mit Rest (nur bis 12:40 min.) (12:40) [CS]
- Euklidischer Algorithmus 02 - Sätze zum ggT, Teil 1 (12:04) [CS]
- Euklidischer Algorithmus 03 - Sätze zum ggT, Teil 2 (13:12) [CS]
- Euklidischer Algorithmus 04 - Euklidischer Algorithmus, Teil 1 (10:47) [CS]
- Euklidischer Algorithmus 05 - Euklidischer Algorithmus, Teil 2 (06:05) [CS]
Vorlesung 13 - Diophantische Gleichungen
- Skript namens "11_Diophantische_Gleichungen-Skript.pdf" unter MATERIALIEN.
- Diophantische Gleichungen 01 - Erweiterter Euklidischer Algorithmus, Teil 1 (18:42) [CS]
- Diophantische Gleichungen 02 - Erweiterter Euklidischer Algorithmus, Teil 2 (08:53) [CS]
- Diophantische Gleichungen 03 - Erweiterter Euklidischer Algorithmus, Teil 3 (10:51) [CS]
- Diophantische Gleichungen 04 - Lösbarkeit (14:35) [CS]
- Diophantische Gleichungen 05 - Lösungen (12:58) [CS]
- Diophantische Gleichungen 06 - Übung (09:49) [CS]
- Wolfram-α: positive Lösungen von 440 x + 198 y = 22000
Vorlesung 14 - Kongruenzen
- Skript namens "12-1_Kongruenzen-Skript.pdf" unter MATERIALIEN.
- Kongruenzen 01 - Begriff (12:02) [CS]
- Kongruenzen 02 - Kongruenz-Kriterium (nur bis 1:14 min.) (01:14) [CS]
- Kongruenzen 03 - Rechenregeln (nur bis 2:27 min.) (02:27) [CS]
- Anwendungen Prüfnummern:
- viele Bspe. unter http://www.pruefziffernberechnung.de
- md5sum für Download unter UNIX / Cygwin unter WIN
- ISBN 13: https://dzone.com/articles/thursday-code-puzzler-isbn
- ISBN 10 und 13 in einem HTML-Formular: https://formvalidation.io/guide/validators/isbn/
- SEPA: IBAN mit Prüfnummer:
Vorlesung 15 - Restklassen
- Skript namens "12-2_Restklassen-Skript.pdf" unter MATERIALIEN.
- Restklassen 01 - Begriff, Teil 1 (ab 4:34 min.) (08:14) [CS]
- Restklassen 02 - Begriff, Teil 2 (06:57) [CS]
- Restklassen 03 - Gleichheit von Restklassen (nur bis 1:22) (01:22) [CS]
- Restklassen 04 - Rechenregeln (13:28) [CS]
- Restklassen 05 - Übung (11:44) [CS]
- Restklassen 06 - Quersummenregeln (14:36) [CS]
Vorlesung 16 - Algebraische Strukturen
- Skript namens "13_Algebraische_Strukturen-Skript.pdf" unter MATERIALIEN.
- Algebraische Strukturen 01 - Intro (erst ab 1:35 min.) (08:37) [CS]
- Algebraische Strukturen 02 - Gruppen (17:29) [CS]
- Algebraische Strukturen 03 - Halbgruppen (12:10) [CS]
- Algebraische Strukturen 04 - Restklassen, Addition (21:23) [CS]
- Algebraische Strukturen 05 - Restklassen, Multiplikation (11:05) [CS]
Vorlesung 17 - Algebraische Strukturen, Sätze von Euler und Fermat
- Algebraische Strukturen 06 - Ringe (07:00) [CS]
- Algebraische Strukturen 07 - Inverse in Restklassen (14:11) [CS]
- Algebraische Strukturen 08 - Inverse / Körper (13:18) [CS]
- Inverses von 5 mod 9? Wolfram-α
- Skript namens "14_Sätze_von_Euler_und_Fermat-Skript.pdf" unter MATERIALIEN.
- Sätze von Euler und Fermat 01 - Eulersche Phi-Funktion (16:31) [CS]
- phi(110) = ? Wolfram-α
- Sätze von Euler und Fermat 02 - Satz von Euler (12:13) [CS]
- Sätze von Euler und Fermat 03 - kleiner Satz von Fermat (06:04) [CS]
- bei Interesse (optional): großer Satz von Fermat: Teil 1 (16:59), Teil 2 (08:50) [CS]
- noch mehr zum großen Satz von Fermat (optional):
- Fermats letzter Satz: Die abenteuerliche Geschichte eines mathematischen Rätsels
bei amazon
- Großer Satz von Fermat auf Wikipedia
- Der große Satz von Fermat - die Lösung eines 300 Jahre alten Problems von Jürg Kramer
- Andrew Wiles auf Wikipedia
- Wolfskehl-Preis auf Wikipedia
Vorlesung 18 - Chinesischer Restsatz
- Skript namens "15_Chinesischer_Restsatz-Skript.pdf" unter MATERIALIEN.
- Chinesischer Restsatz 01 - Intro, Teil 1 (12:38) [CS]
- Chinesischer Restsatz 02 - Intro, Teil 2 (13:55) [CS]
- Chinesischer Restsatz 03 - Satz (12:46) [CS]
- x = 2 (mod 3), x = 7 (mod 10)? Wolfram-α
- Ü [Eieraufgabe des Brahmagupta]: Eine alte Frau geht über den Marktplatz. Ein Pferd tritt auf ihre Tasche und zerbricht die gekauften Eier. Der Besitzer des Pferdes möchte den Schaden ersetzen und fragt die alte Frau, wie viele Eier in ihrer Tasche waren. Sie weiß die exakte Zahl nicht mehr, aber sie erinnert sich, dass genau ein Ei übrig bleibt, wenn sie beim Auspacken die Eier immer zu zweit aus der Tasche nimmt. Das Gleiche geschieht, wenn sie die Eier immer zu dritt, zu viert, zu fünft und zu sechst aus der Tasche nimmt. Nur wenn sie die Eier zu siebt aus der Tasche nimmt, bleibt kein Ei übrig. Was ist die kleinste Zahl an Eiern, welche die alte Frau in ihrer Tasche haben kann?
Vorlesung 19 - Kryptographie
- Skript namens "16-0_Kryptographie-Skript.pdf" unter MATERIALIEN
- Kryptographie 01 - Cäsar-Verschlüsselung (15:42) [CS]
- Kryptographie 02 - Vigenére-Verschlüsselung (11:17, Tabelle siehe: https://de.wikipedia.org/wiki/Polyalphabetische_Substitution) [CS]
- Skript namens "16-1_Kryptographie-RSA.pdf" unter MATERIALIEN
- Kryptographie 03 - Verschlüsselung im Internet mit dem Public-Key-Kryptographie-Verfahren RSA (20:09)
- zurück zu Skript namens "16-0_Kryptographie-Skript.pdf"
- Kryptographie 04 - RSA: Intro (07:49) [CS]
- Kryptographie 05 - RSA: Schlüssel (17:23) [CS]
- Kryptographie 06 - RSA: Ver- und Entschlüsselung (13:50) [CS]
- Kryptographie 07 - RSA: Übung, Teil 1 (10:59) [CS]
- Kryptographie 08 - RSA: Übung, Teil 2 (10:13) [CS]
Ergänzungen:
- Prof. Dr. Otto Forster : http://www.mathematik.uni-muenchen.de/~fmwus/download/ausgabe23.pdf (S. 29-35)
- Prof. Dr. Cornelius Greither: http://www.mathematik.uni-muenchen.de/~fmwus/download/ausgabe19.pdf (S. 28-34)
- aktuelle Schlüssellängen: BSI - Technische Richtlinie: Kryptographische Verfahren: Empfehlungen und Schlussellängen
Vorlesung 20
Relationen
- Skript namens "17_Relationen-Skript.pdf" unter MATERIALIEN.
- Relationen 01 - Intro (ab 3:00 min.) (12:00) [CS]
- Relationen 02 - Definition (ab 1:20 min.) (10:19) [CS]
- Relationen 03 - Eigenschaften, Teil 1 (14:40) [CS]
- Relationen 04 - Eigenschaften, Teil 2 (13:32) [CS]
- Relationen 05 - Übung (11:05) [CS]
- Quiz zu Relationen: Testen Sie Ihr Wissen!
Eigenschaften von Funktionen; lineare Funktionen; Potenz- und Wurzelfunktionen
- Skript namens "18_Eigenschaften,_lineare_Funktionen,_Potenzen,_Wurzeln-Skript.pdf" unter MATERIALIEN
- Funktionen 01 - monotone, gerade, ungerade, periodische Funktionen (13:02) [JL]
- Funktionen 02 - Lineare Funktionen, Achsenabschnittsform (8:56) [JL]
- Funktionen 03 - weiter lineare Funktionen, Steigung, Achsenabschnitt (4:14) [JL]
- Funktionen 04 - Potenzfunktionen (11:08) [JL]
- Funktionen 05 - Wurzelfunktionen (9:24) [JL]
- Funktionen 06 - Rechenregeln für Potenzen und Wurzeln (14:21) [JL]
- Plot der 1/x^n: Wolfram-α
Vorlesung 21 - Exponentialfunktionen, Logarithmen, Eulersche Zahl
- Skript namens "19_Exponentialfunktionen,_Eulersche_Zahl,_Logarithmen-Skript.pdf" unter MATERIALIEN.
- Funktionen 07 - Exponentialfunktionen (10:00) [JL]
- Funktionen 08 - Eulersche Zahl, Exponentialfunktion (12:49) [JL]
- Funktionen 09 - weiter Eulersche Zahl, Exponentialfunktion (14:10) [JL]
- Funktionen 10 - Beispiele Wachstum, Zerfall, Skalen (10:38) [JL]
- optional: Funktionen 11 - Beispiele Boltzmann-Statistik, Diodenkennlinie (14:05) [JL]
- Funktionen 12 - Logarithmen (10:04) [JL]
- Funktionen 13 - Rechenregeln für Logarithmen (10:14) [JL]
- Funktionen 14 - Beispiele Logarithmus; Dezibel, Oktaven, Bits (6:54) [JL]
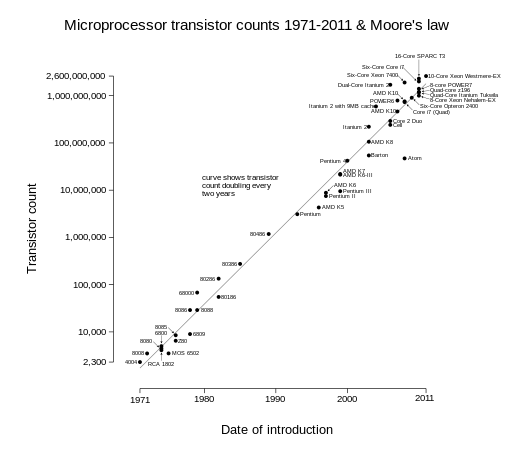
- optional: Funktionen 15 - halblogarithmisches, doppeltlogarithmisches Diagramm (13:05) [JL]
Anwendungen:
- Moore's Law. Alle 2 Jahre verdoppeln sich die Transistoren in einer CPU (Tabelle Anzahl Transistoren):
- Sissa ibn Dahir: Schachbrettaufgabe dazu das Video
- weitere Anwendungen zu Exponentielles Wachstum
Vorlesung 22
Polynome
- Skript namens "20_Polynome-Skript.pdf" unter MATERIALIEN.
- Funktionen 16 - Polynome, Begriffe, Verlauf (8:39) [JL]
- Funktionen 17 - Polynome angewendet, Näherung, Interpolation, Differentialgleichung (14:57) [JL]
- Funktionen 18 - Polynomdivision (9:18) [JL]
- Funktionen 19 - Nullstellen und Linearfaktoren (10:00) [JL]
- Funktionen 20 - weiter Nullstellen und Linearfaktoren (6:20) [JL]
- optional: Funktionen 21 - Horner-Schema (3:17) [JL]
Sinus und Freunde, Arcusfunktionen
- Skript namens "21_Sinus_und_Freunde,_Arcusfunktionen-Skript.pdf" unter MATERIALIEN.
- Funktionen 22 - Rechtwinkliges Dreieck, Hypotenuse, Kathete, Pythagoras (5:51) [JL]
- Funktionen 23 - Sinus, Cosinus, Tangens, Cotangens (14:01) [JL]
- Funktionen 24 - Bogenmaß, Gon (7:46) [JL]
- Funktionen 25 - Sinus, Cosinus, Tangens am Einheitskreis (8:02) [JL]
- optional: Funktionen 26 - Sinussatz (8:10) [JL]
- optional: Funktionen 27 - Cosinussatz (12:13) [JL]
- Funktionen 28 - arcsin, Arcussinus (9:21) [JL]
- Funktionen 29 - arccos, arctan, Arcuscosinus, Arcustangens (14:57) [JL]
- optional: Funktionen 30 - atan2, Arcustangens (2:46) [JL]







No comments:
Post a Comment